이 글은 블로킹과 논블로킹에 대한 이해를 바탕으로 블로킹 커뮤니케이션(Bloking communications)의 예제를 다뤘다.
MPI 코드로 수치적분을 구현한 원본게시글을 따라가며 이해한 내용들을 기록한 문서이다.
I MPI 블로킹 커뮤니케이션과 수치적분
- Numerical Integration wtih MPI Blocking Communications
MPI 블로킹 커뮤니케이션을 예제로 평범하고 하찮은(원본이 이렇게 소개한다.) 그리고 간단한 알고리즘인 수치적분법을 가져왔다. 평범하고 하찮으며 간단한 알고리즘이라하더라도 필자와 같은 사람은 모를 수 있기에 간단한 설명을 하겠다. 이미 훤히 알고있다면 I.2 로 바로넘어가자.
I.1 수치적분
어떤 식 혹은 데이터를 적분하는데, 일반적인 식을 유도하는 방법이 어려울때 적분을 사칙연산으로 하겠다는 것이다. 여기선 자세히 설명하지 않으니보다 자세한 사항을 알고싶다면 위키피디아 및 다른 설명을 참고하시라. 여하튼 학창시절 배운 구분구적법과 방법론이 거의 동일하다. 대신 거기서 범위를 무한하게 쪼개는 것이 아니라, 유한하게 나누어 더하는, 일종의 근사식이다. 아래 식에서 lim 가 빠져있을뿐이다.

흠, 간단한 이해를 위해 그림과 같이 설명하면, 그림처럼 곡선으로된 함수를 사각형으로 나눠 Δx 와 그에 해당하는 f(x)로 사각형의 넓이를 구해서 다 더하는 거다.
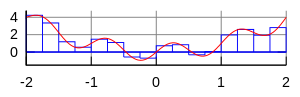
개념에대한 설명이 부족하지만 아래서 구현된 알고리즘을 따라가면서 이해하면 다른 포스팅을 찾는것 보다 빠르지 싶다.
수치적분 예시가 병렬로 쉽게 처리될 수 있는 이유도 생각해 봐야한다. 뭐, 수치적분은 단순 더하기 계산이기에 가능하다. 가령 위 예시를 아래처럼 범위를 나눠 사각형 넓이를 다 더한다고 생각해보자. 모든 사각형의 넓이를 한번에 더하는것과 같을 것이다. 왜냐고 묻는다면 덧샘의 분배법칙, 결합법칙, 그리고 교환법칙에 의거하여. 라는 유식한(초등학교때 배웠는데 저 단어들을 이해할 수 없었다) 언어로 얘기하겠다.어쨋든 가능하다...! 가능~☆
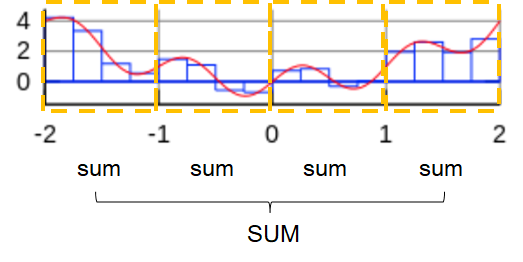
I.2 포트란 + MPI 코드 및 실행결과
C 코드도 원본 포스팅에 함께 첨부되어있으니, C 사용자라면 참고하길 바란다.
Program Example1_1
!#######################################################################
!# #
!# This is an MPI example on parallel integration to demonstrate the #
!# use of: #
!# #
!# * MPI_Init, MPI_Comm_rank, MPI_Comm_size, MPI_Finalize #
!# * MPI_Recv, MPI_Send #
!# #
!# Dr. Kadin Tseng #
!# Scientific Computing and Visualization #
!# Boston University #
!# 1998 #
!# #
!#######################################################################
implicit none
integer n, p, i, j, proc, ierr, master, myid, tag, comm
real h, a, b, integral, pi, ai, my_int, integral_sum
include "mpif.h" ! brings in pre-defined MPI constants, ...
integer status(MPI_STATUS_SIZE) ! size defined in mpif.h
data master/0/ ! 최종 합계를 할 마스터(0) 프로세서를 지정
comm = MPI_COMM_WORLD
call MPI_Init(ierr) ! MPI 기능 활성화
call MPI_Comm_rank(comm, myid, ierr) ! 현재 프로세서 ID 가져오기
call MPI_Comm_size(comm, p, ierr) ! 총 프로세서 개수 가져오기
pi = acos(-1.0) ! = 3.14159...
a = 0.0 ! 적분 하한
b = pi/2. ! 적분 상한 (a~b까지 적분)
n = 500 ! 한 프로세서가 부여받은 범위를 나눌 계산 간격 수
tag = 123 ! 로컬 적분 합을 송수신 용 TAG 값 설정
h = (b-a)/n/(p) ! 간격의 길이
if (myid .ne. 0) then
ai = a + (myid-1)*n*h ! lower limit of integration for partition myid
my_int = integral(ai, h, n)
write(*,"('Process ',i2,' has the partial sum of',f10.6)")
& myid,my_int
call MPI_Send(
& my_int, 1, MPI_REAL, ! 버퍼, 데이터사이즈, 데이터타입
& master, ! 메시지를 보낼 프로세서 번호
& tag, ! 위에서 설정한 TAG 값
& comm, ierr)
else
print *, '\n## Main program ##'
integral_sum = 0.0 ! 총계 변수 초기화
do proc=1,p-1 ! 각 로컬 프로세서의 합계 수신
write(*,*) proc
! 메시지가 오지 않았을 시 수신될때까지 기다림 (Blocking)
call MPI_Recv(
& my_int, 1, MPI_REAL,
& proc, ! 메시지를 보내는 프로세서 번호
& tag, ! 위에서 설정한 TAG 값
& comm, status, ierr)
integral_sum = integral_sum + my_int
print *, my_int,' is added, and total sum is ', integral_sum
enddo
print *,'The integral =',integral_sum
endif
call MPI_Finalize(ierr) ! MPI finish up ...
stop
end
!
!
real function integral(ai, h, n)
implicit none
integer n, j
real h, ai, aij
integral = 0.0 ! initialize integral
do j=0,n-1 ! sum integrals
aij = ai +(j+0.5)*h ! abscissa mid-point
integral = integral + cos(aij)*h
enddo
return
end
코드에 달린 주석과 함께 읽어보면 MPI가 어떻게 돌아가는지 감을 잡을 수 있지만, 간단한 설명을 덧붙이도록 하겠다.
코드를 보기 전에 MPI 코드를 구동하는 방법을 보자. 일반적으로 사용할 프로세서의 수를 초기화하면서 코드를 구동하게 되는데, 커맨드라인에 $mpirun -np 4 program.out 을 입력한다. 여기서 np는 number of processors의 약자이고 program.out을 4개의 프로세서를 사용해 실행하겠다는 옵션이다. MPI 코드를 실행할때 많이 사용하게 될 것임으로 기억해 두는 것이 좋다.
이제 코드 안을 들여다보자. 4개의 프로세서를 쓰기로 했으니, 각 프로세서가 어떤 역할을 할지 정해줘야한다. 그러려면 각 프로세서를 구분해야하는데, 현재 프로세서 번호인 myid를 쿼리하면 된다. call MPI_Init(ierr)을 통해 MPI 기능을 활성화 하면, 4개의 프로세서가 아래 코드를 수행하기 시작한다. 여기서 현재 프로세서 ID를 불러와 myid를 찾을 수 있다.
call MPI_Init(ierr) ! MPI 기능 활성화
call MPI_Comm_rank(comm, myid, ierr) ! 현재 프로세서 ID 가져오기
call MPI_Comm_size(comm, p, ierr) ! 총 프로세서 개수 가져오기
예제 내에서 프로세스 간 송수신은 MPI_Send 및 MPI_Recv 블로킹 쌍으로한다. 즉, 이를 통해 각 프로세서에서 구한 로컬적분합계를 0번 프로세서(메인)에서 총합을 구하도록 전달하게 되겠다. 그리고, 마지막에 MPI_Finalize를 통해 프로그램을 종료하기 전에 MPI를 안전하게(순서대로) 종료한다.
위 코드를 달린 주석과 함께 뜯어보면, MPI가 어떻게 돌아가는지 대충 감을 잡을 수가 있다. 코드를 대충 이해했다면 컴파일, 그리고 실행을해보자. mpif90을 통해 컴파일을 해주고
$mpif90 MPI_integration.for -o MPI_integration.exe -I/<mpif.h 위치>
프로세서를 몇개 쓸지(-np, number of processor)를 설정하여 코드를 실행해 준다.
$mpirun -np 4 MPI_integration.exe
결과로 다음과 같이 출력되었
$ mpirun -np 4 ./ex_2.exe
Process 1 has the partial sum of 0.382684
Process 2 has the partial sum of 0.324423
Process 3 has the partial sum of 0.216773
\n## Main program ##
1
0.38268363 is added, and total sum is 0.38268363
2
0.32442346 is added, and total sum is 0.70710707
3
0.21677256 is added, and total sum is 0.92387962
The integral = 0.92387962
으면 좋겠는데, 아래와 같이 뒤죽박죽 섞여서 출력되었다. 다른 예제들에서는 마스터 프로세서 외 프로세서들이 번호 순서대로 진행되어서, 위 예상 결과처럼 출력됬는데...
$mpirun -np 4 ./ex_2.exe
\n## Main program ##
1
Process 2 has the partial sum of 0.324423
Process 3 has the partial sum of 0.216773
0.38268363 is added, and total sum is 0.38268363
2
0.32442346 is added, and total sum is 0.70710707
3
0.21677256 is added, and total sum is 0.92387962
The integral = 0.92387962
Process 1 has the partial sum of 0.382684
마스터 코드에서는 기다리고 있다가 MPIsend가 오는 족족 받아서 더하는구나... ^^ 여하튼 해석해를 구하면 적분값이 1이 나와야 하지만, 범위를 1,500(3*500)개 구간으로 나눠 적분시 약 0.92 정도나온다. 그래서 간격 개수를 늘려 6,000(12*500)개로 나누면, 약 0.99 정도로 1퍼센트 미만의 정확도가 나온다.
$mpirun -np 13 ./ex_2.exe
Process 3 has the partial sum of 0.115289
Process 2 has the partial sum of 0.118779
Process 6 has the partial sum of 0.095058
Process 12 has the partial sum of 0.021767
Process 7 has the partial sum of 0.085388
Process 10 has the partial sum of 0.049560
Process 5 has the partial sum of 0.103342
Process 11 has the partial sum of 0.035926
Process 4 has the partial sum of 0.110118
\n## Main program ##
1
Process 1 has the partial sum of 0.120537
Process 9 has the partial sum of 0.062472
0.12053668 is added, and total sum is 0.12053668
2
0.11877900 is added, and total sum is 0.23931569
3
0.11528926 is added, and total sum is 0.35460496
4
0.11011832 is added, and total sum is 0.46472329
5
0.10334162 is added, and total sum is 0.56806493
6
9.50578898E-02 is added, and total sum is 0.66312283
7
8.53881091E-02 is added, and total sum is 0.74851096
8
Process 8 has the partial sum of 0.074473
7.44730979E-02 is added, and total sum is 0.82298404
9
6.24721237E-02 is added, and total sum is 0.88545614
10
4.95602340E-02 is added, and total sum is 0.93501639
11
3.59255672E-02 is added, and total sum is 0.97094196
12
2.17670593E-02 is added, and total sum is 0.99270904
The integral = 0.99270904
**사실 원본의 코드에서 조금 바꿨다. 이 게시글의 코드에는 마스터 프로세서에서 로컬합 계산을 하지 않도록 해 두었다. 원본의 코드도 함께 첨부하니, 그 차이점을 잘 생각해 보면 좋을 것이다.
Program Example1_1
c#######################################################################
c# #
c# This is an MPI example on parallel integration to demonstrate the #
c# use of: #
c# #
c# * MPI_Init, MPI_Comm_rank, MPI_Comm_size, MPI_Finalize #
c# * MPI_Recv, MPI_Send #
c# #
c# Dr. Kadin Tseng #
c# Scientific Computing and Visualization #
c# Boston University #
c# 1998 #
c# #
c#######################################################################
implicit none
integer n, p, i, j, proc, ierr, master, myid, tag, comm
real h, a, b, integral, pi, ai, my_int, integral_sum
include "mpif.h" ! brings in pre-defined MPI constants, ...
integer status(MPI_STATUS_SIZE) ! size defined in mpif.h
data master/0/ ! processor 0 collects integral sums from other processors
comm = MPI_COMM_WORLD
call MPI_Init(ierr) ! starts MPI
call MPI_Comm_rank(comm, myid, ierr) ! get current proc ID
call MPI_Comm_size(comm, p, ierr) ! get number of procs
pi = acos(-1.0) ! = 3.14159...
a = 0.0 ! lower limit of integration
b = pi/2. ! upper limit of integration
n = 500 ! number of increment within each process
tag = 123 ! set the tag to identify this particular job
h = (b-a)/n/p ! length of increment
ai = a + myid*n*h ! lower limit of integration for partition myid
my_int = integral(ai, h, n)
write(*,"('Process ',i2,' has the partial sum of',f10.6)")
& myid,my_int
call MPI_Send(
& my_int, 1, MPI_REAL, ! buffer, size, datatype
& master, ! where to send message
& tag, ! message tag
& comm, ierr)
if(myid .eq. master) then ! do following only on master ...
integral_sum = 0.0 ! initialize integral_sum to zero
do proc=0,p-1 ! loop on processors to collect local sum
call MPI_Recv(
& my_int, 1, MPI_REAL,
& proc, ! message source
& tag, ! message tag
& comm, status, ierr) ! status reports source, tag
integral_sum = integral_sum + my_int ! sum my_int from processors
enddo
print *,'The integral =',integral_sum
endif
call MPI_Finalize(ierr) ! MPI finish up ...
end
real function integral(ai, h, n)
implicit none
integer n, j
real h, ai, aij
integral = 0.0 ! initialize integral
do j=0,n-1 ! sum integrals
aij = ai +(j+0.5)*h ! abscissa mid-point
integral = integral + cos(aij)*h
enddo
return
end'Engineer > 병렬컴퓨팅' 카테고리의 다른 글
| 5. 유도데이터타입(CONTIGUOUS), 예제로 배우기 (0) | 2020.03.24 |
|---|---|
| 4. 집합통신-2, 예제(수치적분)로 배우기 (0) | 2020.03.24 |
| 3. 집합통신, 예제(수치적분)로 배우기 (0) | 2020.03.24 |
| 2. 논블로킹 통신, 예제(수치적분)로 배우기 (0) | 2020.03.24 |
| 포트란으로 MPI 배우기 (0) | 2020.03.19 |




댓글