링크의 내용을 공부하며 제멋대로 번역한 내용입니다.
기본편은 이 글이 마지막 글이며, 링크에 보간법, 수치적분법, FFT 관련 내용도 있으니 참고바랍니다.

수치해석을 하려면 이제 행렬을 푸는 방법을 알아야한다. 얼마나 빠르고 정확하게 행렬식의 해를 구할 수 있는가는 수치해석의 처음과 끝이다. FEM을 풀던 FDM, FVM, 등 뭐를 풀던 똑같다.
EXAMPLE PROB. LAPLACIAN EQU.
예제 라플라시안 방정식
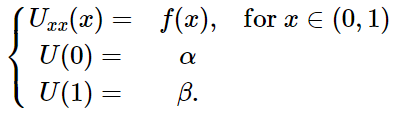
자 격자를 M+1개로 나눈다. 즉 포인트는 M+2개가 되겠다. (0,1,2..., M, M+1)
그리고 Uxx를 2차 중앙 차분을 하면 아래와 같다.

각 경계조건은 알파와 베타이니까, u0 = alpha, u_(m+1) = beta로 놓고 행렬식을 정리하면 다음과 같다.

자 여기서 h는 격자 하나의 크기가 되겠다.
INITIALIZING FDM MATRIX 유한차분법 행렬 초기화
자 이제 수학적으로는 문제 정의를 마쳤으니, 코드상에 이를 구현해보자.
#PROBLEM DEFINITION
\alpha = 1;
\beta = 1;
f(x) = exp(x)
# CREATE uniform mesh
m = 1000;
h = 1/(m+1);
x = LinRange(0,1,m+2)
x_inner = x[2:m+1]A 행렬을 쉽게 짜기 위해서는 아래처럼 반복문을 사용하면 쉽다.
# ELEMENTS of TRIDIAGONAL MATRIX
function fillmat!(A)
for i=1:m
A[i,i] = -2
if i<m
A[i,i+1] =1
end
if i>1
A[i,i-1] =1
end
end
end
# Fill Matrix A
A = Matrix{Float64}(undef,m,m)
fillmat!(A)
# CREATE b vector
B = Array{Float64}(undef,m,m)
for i=1:m
B[i] = h^2 * f(x_inner[i])
end
B[1] = B[1] - \alpha
B[m] = B[m] - \beta여기서 행렬A와 백터b의 크기가 m+2가 아닌이유는 경계조건 때문이다. 경계조건은 이미 정의가 되어 있으므로 1, m번째 행렬에 고려하여 식을 추가한 것이다. (위 코드 마지막 2줄 참고)
SOLVING PROB 행렬식 풀기
내장 역행렬 솔버 backslash
가장 쉬운 방법은 이미 줄리아에 내장되어 있는 역슬래쉬(backslash) 구문으로 푸는 것이다. 간단하지만... 좀 시간이 걸리지 싶다!
u = A\B;해석해와 비교하기 위해 플랏 까지!
a = - exp(0) + \alpha;
b = \beta - a - exp(1);
u_exact(x) = exp(x) + a + b*x
using Plots
plot(x,u_exact.(x), marker=8, markeralpha =0.1, label="Exact Solution")
plot!(x,[\alpha; u; \beta] marker=4, label="Numerical Solution")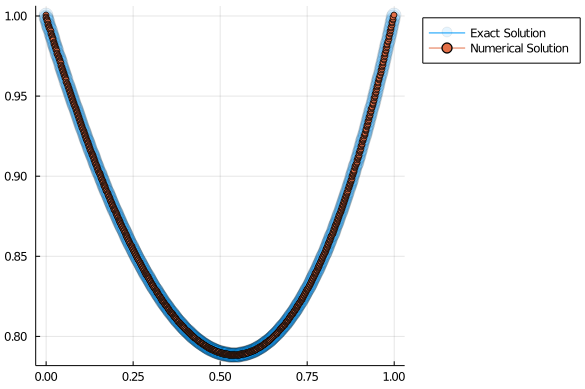
Plots 패키지를 첨읽어올 떄 좀 느리긴 하다. 근데 sysimage라는 거로 미리 컴파일 해놓을 수 있다그래서 나중에 다뤄보도록 하겠다.
LU Decomposition
그냥 역슬래시 기법말고 LU디컴포지션으로도 해를 구할 수 있다. 뭐 전체적으로 보면 역슬레시 기법이랑 큰 계산시간 차이가 안나지만, 미리 식을 디컴포지션/나눠놓는데 시간이 할애되므로, 여러번 반복해서 풀어야한다면 빠르게 구할 수 있다는 장점이 있다.
그러니까
Ax = b를 LUx = Pb 형태로 바꿔놓는데 시간이 좀 들긴 하지만 이렇게 바꾼 후로는 연산이 빨라진다는 것이다.
b는 바뀌어도 상관이 없으니 L,U,P를 저장해놓고 여러번 반복 계산할때 유리하다.
using LinearAlgebra
lufact = lu(A);
lufact.L
lufact.U
lufact.p
or
L,U,p = lu(A);이렇게 L,U,P를 구한다!
그러면 아래처럼 구할 수 있다. LinearAlgebra 패키지가 제공해주는 듯 ?
luA = lu(A);
x = luA\B;디컴포지션 이 후 과정을 한번에 처리해준다. 그르니까 이 두줄을 해석하면 그냥 역슬래쉬로 계산하는 것과 큰 차이가 없는데, 아래 식만 계산하는것은 거의 5프로 수준의 시간, 무시가능한 시간만 차지한다는 말이다.
SPARSE MATRICES 희소행렬
수치해석을 하다보면 행렬에 0값이 많은 희소행렬이 주를 이룬다. 그래서 희소행렬이라는 것을 사용하는데, 행렬을 저장하는데 N*N 메모리가 아니라 그보다 70% 이상 줄일 수 있다. 줄리아는 이 기능을 쉽게 요롷게 해준다.
A = Matrix{FLoat64}(undef,m,m)
fillmat!(A)
As = saprse(A);A의 요소들을 다루기는 어려워 지지만 효율적으로 행렬을 저장할 수 있다! 심지어 행렬객체와 혼용해서 사용한다..... 아래가 가능하다.... 굳이 새로운 fillmat!을 정의할 필요가 없다.
As = spzeros(m,m)
fillmat!(As)
원본의 저자는 다음과 같은 케이스를 테스트 해봤다.
function get_vectors(m)
II,JJ,V = [Array{Float64}(undef,0) for _ in 1:3]
for i = 1:m
push!(II,i); push!(JJ,i) push!(V,-2)
if i<m
push!(II,i); push!(JJ,i+1); push!(V,1);
end
if i>1
push!(II,i); push!(JJ,i-1); push!(V,1);
end
end
return II,JJ,V
end
II,JJ,V = get_vectors(m)
As = sparse(II,JJ,V)이렇게 백터로 변수를 정의해서 희소행렬을 만들면 첫번째 방법(A를 만들고 스파스로 바꾸기)보다 15.78배 빠르다. 반면 spzeros로 As 초기화하고 스파스로 희소행렬을 자동으로 만든 것은 첫번째 방법보다 3.76배 빨랐다. 즉, 백터로 만들어서 스파스로 만드는게 훨씬 빠르다는 것이다.(사실 당연하다 매트릭스를 스파스로 스케일 다운하는 작업이 더 들어가니까..... 백터로 만들면 그냥 그게 희소행렬이 되니까!)
그러면 0으로 꽉차있던 기존 Dense 행렬보다 희소행렬이 역행렬을 구하느게 더 빠를까? 줄리아에서 그렇다고 한다.
using Linear Algebra
A = fillmat!(Matrix{Float64}(undef,m,m));
As= sparse(A);
luA = lu(A)
luAsp = lu(As)
x = luA\B
x = luAsp\B스파스로 했을 때가 스피드업이 13배이다..... 즉, 스파스 메트릭스로 정의하고 계산하면 무지 빠르다눈그런말이다....
ITERATIVE METHODS 반복법
사실 실제 상용 수치해석프로그램에서는 반복법을 이용한 행렬솔버를 쓴다. Bi-CGSTAB같은(이것도 줄리아에 있따!)! 보통 매우 큰 행렬을 풀기 때문인데, N*N 매트릭스를 풀기위해서 드는 계산량 때문에 근사적으로 해를 풀 필요가 있다. 줄리아도 물론 반복법 패키지를 제공한다. IterativeSolvers는 LINEAR SYSTEM, EIGENSYSTEM, SINGULAR VALUE PROB 까지 푸는 일반적인 솔버들을 제공한다.
using IterativeSolvers만약 패키지가 없다면 줄리아 터미널에서 아래 명령어를 사용하자.
using Pkg
Pkg.add("PakageName")
어쨋든 패키지 임포트를 했다면, 예제를 보자. 원문 예제는 GMRES(Generalized minimal residual method)기법을 사용했다. nonsingular 문제에 적용할 수 있다고 한다. 아무튼 예제는 다음과 같다. iter_a(x)는 앞선 Ax=B예제의 Ax를 한번에 구한 것이다. x를 인풋으로 받도록 말이다.
iter_A(x) = [ -2x[1] + x[2]; x[1:end-2] - 2x[2:end-1] + x[3:end] ; -2x[end] + x[end-1] ]초기 예측값을 xt로 놓고... 잘 계산되는지 보자
xt = rand(m);
norm(iter_A(xt) - A*xt)이렇게 하면 거의 0 값으로 나오니 계산은 잘 되고 있다고 보자
이제 GMRES를 사용해 해를 구해보자. 그러기 위해서는 보통 LinearMaps라는 패키지가 필요하단다.
using LinearMaps
Ax = LinearMaps(x->iter_A(x),m,m)
x_gmres = gmres(Ax,B,reltol=1e-8,restart=m)
norm(x_gmres-u)요롷게 사용할 수 있따. restart는 m번 이상 반복법이 돌면 다시 시작하라는 것이다.. 마지막 코드가 벡슬래시로 구한 값과 차이를 비교한 것인데, 1e-8수준에서 정확도가 나오는 걸 보면 잘 된것 같다....
'Engineer > Juila' 카테고리의 다른 글
| [Julia] 기본2 - 2. 코드 최적화하는 법 (0) | 2021.10.29 |
|---|---|
| [Julia] 기본2 - 1. 구조체 기본 정의법(outer/inner constructor) (0) | 2021.10.12 |
| [Julia] 기본1 - 5. 행렬 가지고 놀기! (0) | 2021.10.11 |
| [Julia] 기본1 - 4. 함수 사용하기 (0) | 2021.10.11 |
| [Julia] 기본1 - 3. 반복문(Loop 문) 사용하기 (0) | 2021.10.11 |




댓글